Fitxa dels nombres enters I

En aquesta secció veurem la utilitat dels nombres enters i aprendrem a usar la seva notació correctament.

Presentació

Exemples previs de nombres enters al nostre entorn:

• Mesura de la temperatura: el termòmetre i les línies isotèrmiques:

• Càlcul dels anys:

<timeline> DateFormat = yyyy ImageSize = width:800 height:350 PlotArea = left:20 right:20 bottom:20 top:0 Colors = id:canvas-bar value:rgb(0.97,0.97,0.97) id:grid_minor value:rgb(0.86,0.86,0.86) id:grid_major value:rgb(0.80,0.80,0.80) id:live_exthe value:lightorange legend:Extrahelenístico id:live_inthe value:dullyellow legend:Helenístico id:live_jesus value:red id:live_posje value:lavender legend:Poscristiano id:fact_inthe value:teal Period = from:-400 till:100 TimeAxis = orientation:horizontal format:yyyy AlignBars = justify ScaleMinor = unit:year increment:10 start:-390 gridcolor:grid_minor ScaleMajor = unit:year increment:20 start:-400 gridcolor:grid_major BackgroundColors = canvas:canvas-bar bars:canvas-bar Legend = orientation:vertical left:39 top:84 BarData= barset:inventions PlotData= barset:inventions width:17 from:-384 till:-322 text:"Aristóteles" color:live_exthe anchor:from from:-356 till:-323 text:"Alejandro Magno" color:live_exthe anchor:from from:-341 till:-270 text:"Epicuro" color:live_inthe anchor:from from:-333 till:-264 text:"Zenón de Citio" color:live_inthe anchor:from from:-305 till:-282 text:"Ptolomeo I" color:live_inthe anchor:from from:-276 till:-195 text:"Eratóstenes" color:live_inthe anchor:from from:-196 till:-196 text:"_Piedra de Rosetta" color:fact_inthe anchor:from from:-181 till:-145 text:"Ptolomeo VI" color:live_inthe anchor:from from:-133 till:-133 text:" Conquista de Numancia" color:fact_inthe anchor:from from:-100 till:-44 text:"Julio César" color:live_inthe anchor:from from:-83 till:-30 text:"Marco Antonio" color:live_inthe anchor:from from:-69 till:-30 text:"Cleopatra" color:live_inthe anchor:from from:-44 till:-30 text:"Ptolomeo XV" color:live_inthe anchor:from from:-20 till:50 text:"Filón de Alejandría" color:live_exthe anchor:from from:-4 till:29 text:"Jesús de Nazaret" color: from:live_posje anchor:from till:30 text:"Séneca" color:live_posje anchor:from from:37 till:68 text:"Nerón" color:live_posje anchor:from from:38 till:94 text:"Flavio Josefo" color:live_posje anchor:from </timeline>

• Fusos horaris:

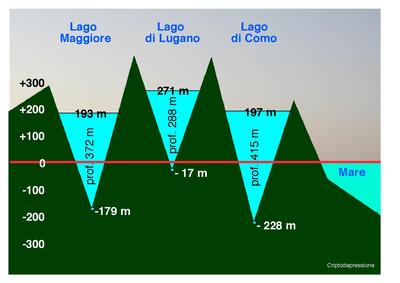
• Mesura de l'alçaria respecte del nivell del mar:

• L'ascensor: panell d'accés al aparcament.

• Índex borsaris: Imatge fixa(no actualitzada).

Bolsa	Valor	Variación	Variación(%)
IBEX 35	8.924,00	-117,10	-1,29%
Futuros S&P 500	2.920,88	-16,62	-0,57%
Futuros Nasdaq	7.697,25	-42,75	-0,55%
Dow 30	26.478,02	-95,70	-0,36%
DAX	11.967,90	-129,53	-1,07%
Índice dólar	98,595	-0,070	-0,07%
Índice euro	95,89	+0,16	+0,16%
Futuros Bitcoin	8.190,0	-65,0	-0,79%

• Saldo bancari.

Per exemple nombres positius per un saldo i nombres negatius per indicar deutes.

• El contrari d'afegir o +1 és extreure o -1.

• El contrari de sumar o +1 és restar o -1.

• El contrari d'avançar o +1 és retrocedir o -1.

I així successivament.

Ordenació

Per construcció de la recta numèrica només cal dir que sempre els de la dreta són més grans que els de l'esquerra. Concretament:

• Donat un número qualsevol, tot número situat a l'esquerra és més petit i tot número situat a la dreta és més gran.

Símbols per expressar o indicar l'ordre entre els nombres i particularment els enters:

• El símbol següent entre les lletres $a>b$ indica que:

a és més gran que b o

b és més petit que a.

• El símbol següent entre les lletres $a<b$ indica que:

a és més petit que b o

b és més gran que a.

• El símbol següent entre les lletres $a⩾b$ indica que:

a és més gran que b i inclús podria ser igual o

b és més petit que a i inclús podria ser igual.

• El símbol següent entre les lletres $a⩽b$ indica que:

a és més petit que b i inclús podria ser igual o

b és més gran que a i inclús podria ser igual.

Sumes i restes

La operació suma i resta com a notació signe usant la recta numèrica:

Exemple

a) +1+3-2+5-4=+3=3 b) +5-2-2-2=-1 c) -3+6-7+8-9=-5 d) -10+3+3+3+3=+2=2

e) -3-4-5-6-7=-25 f) -1+1-1+1-1+1-1+1=+0=0 g) -9+8+8-9=-2 h) -2+3+3-2+3+3-2=+6=6

Exercicis

1) -3-5+7-0 =

2) -7+6+0 =

3) -10+4-10+8-10+6 =

4*) 1-2+3-4+5-6+7-...+61-62 =

5) Un dofí dins del mar ascendeix 200 metres per caçar, després descendeix 400 metres tot seguit ascendeix 300 metres i, després de voltar, torna a ascendir 300 metres on roman quiet una estona i finalment ascendeix 200 metres arribant a la superfície del mar.

a) Feu un esquema ideal del recorregut del dofí.

b) A quina profunditat es trobava inicialment?

6) Un ascensor avariat té adaptat un panell temporalment que no és gens adequat, llavors quan puja ho fa de 3 en 3, i quan baixa ho fa de 5 en 5. S'ha d'esbrinar la suma que dona el resultat demanat en aquest edifici com indica l'esquema:

🌞
		+5
		+4
		+3
	👫	+2
		+1
🌲🌴		+0		🚗
		-1	🏃
	🧍	-2

a) Es vol pujar del pis -1 al pis 5e.

b) Es vol pujar del pis -2 al pis 5e.

a) Es vol baixar del 2n pis al 1r.

Producte de signes

Aquesta taula s'ha de memoritzar, perquè serveix per multiplicar, dividir i simplificar parèntesis.

$+\times +=+$ $-\times +=-$ $+\times -=-$ $-\times -=+$

¿Per què serveix i on el veurem?

Si tenim +15 € i es quadruplica, és a dir que es multiplica per 4, llavors fem (+15)⨯(+4)=+60 € i no hi ha més, no pot sortir negatiu.

Si tenim un deute de -200 € i multipliquem aquest per 3, llavors el que volem fer és (-200)⨯(+3)=-600 que significa de tenim un deute i és de -600 € i l'ordre no importa també (+3)⨯(-200)=-600 € però ha de ser negatiu sinó vol dir que guanyem i això no pot ser.

Simplificació de parèntesis

És freqüent trobar parèntesis amb un sol terme dins com -(-2), (-3), -(9) o (5), es pot interpretar com -(-2), +(-3), -(+9) o +(+5) respectivament ja que tot nombre sense signe és positiu.

Mètode de simplificació: s'identifiquen els signes de dins i de fora del parèntesis i es multipliquen amb la taula.

Vegem-ho directament amb exemples explicats:

1)

a) $-(-2)$ $=\stackrel{-\times -=+}{\overbrace{-(-}}2)$ $=+2$ $=2$ b) $-(+5)$ $=\stackrel{-\times +=-}{\overbrace{-(+}}5)$ $=-5$ c) $+(-8)$ $=\stackrel{+\times -=-}{\overbrace{+(-}}8)$ $=-8$ d) $+(+11)$ $=\stackrel{+\times +=+}{\overbrace{+(+}}11)$ $=+11$ $=11$ e) $+(-0)$ $=\stackrel{+\times -=-}{\overbrace{+(-}}0)$ $=-0$ $=0$ El zero és l'únic número en el que el signe no és rellevant, sobretot per que no es pot confondre amb un altre enter. 6) $(-4)$ $=\stackrel{+\times -=-}{\overbrace{+(-}}4)$ $=-4$ f) $-(7)$ $=\stackrel{-\times +=-}{\overbrace{-(+}}7)$ $=-7$ g) $(10)$ $=\stackrel{+\times +=+}{\overbrace{+(+}}10)$ $=+10$ $=10$

2) $-(+(-9))$ $=-(\stackrel{+\times -=-}{\overbrace{+(-}}9))$ $=-(-9)$ $=\stackrel{-\times -=+}{\overbrace{-(-}}9)$ $=+9$ $=9$

3) $-(-(-1))$ $=-(\stackrel{-\times -=+}{\overbrace{-(-}}1))$ $=-(+1)$ $=\stackrel{-\times +=-}{\overbrace{-(+}}1)$ $=-1$

Exercicis

1) $+(+11)=$ 2) $+(-100)=$ 3) $-(+51)=$ 4) $-(-3)=$

5) $(-12)=$ 6) $(2)=$ 7) $-(8)=$ 8) $-(-(-2))=$

Multiplicació

Per multiplicar dos nombres enters només cal multiplicar els signes amb la taula i després multipliquem els nombres, vegem-ho amb exemples:

a) $(+2)\times (+2)$ $=+2\times 2$ $=+4$ $=4$ b) $(-4)\times (+2)$ $=-4\times 2$ $=-8$ c) $(+2)\times (-3)$ $=-2\times 3$ $=-6$ d) $(-3)\times (-5)$ $=+3\times 5$ $=+15$ $=15$

e) $-(+2)\times (+5)$ $=-(+2\times 5)$ $=-(+10)$ $=-10$ f) $-(+3)\times (-1)$ $=-(-3\times 1)$ $=-(-3)$ $=+3$ $=3$ g) $-(-2)\times (+6)$ $=-(-2\times 6)$ $=-(-12)$ $=+12$ $=12$ h) $-(-7)\times (-3$ $)=-(+7\times 3)$ $=-(+21)$ $=-21$

Exercicis:

1) $-(+5)\times (+5)=$ 2) $-(-5)\times (-3)=$ 3) $-(+7)\times (-4)=$ 4) $-(-10)\times (+7)=$

5) $-(+2)\times 2=$ 6) $-2\times 8=$ 7) $-4\times (-5)=$ 8) $-(-5)\times 11=$

Divisió

En la divisió succeeix exactament el mateix, els signes es multipliquen i els nombres es divideixen com indica la operació, com per exemple:

a) $(+16)÷(+2)$ $=+16÷2$ $=+8$ $=8$ b) $(-4)÷(+2)$ $=-4÷2$ $=-2$ c) $(+9)÷(-3)$ $=-9÷3$ $=-3$ d) $(-25)÷(-5)$ $=+25÷5$ $=+5$ $=5$

e) $-(+35)÷(+5)$ $=-(+35÷5)$ $=-(+7)$ $=-7$ f) $-(+3)÷(-1)$ $=-(-3÷1)$ $=-(-3)$ $=+3$ $=3$ g) $-(-18)÷(+6)$ $=-(-18÷6)$ $=-(-3)$ $=+3$ $=3$ h) $-(-27)÷(-3)$ $=-(+27÷3)$ $=-(+9)$ $=-9$

Exercicis:

1) $-(+100)÷(+5)=$ 2) $-(-21)÷(-3)=$ 3) $-(+64)÷(-4)=$ 4) $-(-10)÷(+2)=$

5) $-100÷5=$ 6) $-(-21)÷(-(-3))=$ 7) $-64÷(-4)=$ 8) $-(-10)÷2=$

9) La temperatura d'un poble era 20 graus centígrads i es registres les següents variacions o oscil·lacions de temperatura fins a l'actualitat amb la taula:

a) -7

b) +6

c) -9

d) +10

e) -6

f) +5

g) -10

h) +11

Quina temperatura té actualment el poble?

Potències

Ja havíem vist les potencies amb nombres naturals, es a dir amb els nombres $\mathbb{N}=\{1,2,3,4,5,6,7,8,9,10,11,\dots \}.$

$a^n=\underset{nvegades}{\underbrace{a\times \dots \times a}}=b$

Per fer el mateix amb els enters només cal vigilar amb els nombres negatius, per exemple:

a) $(-2{)}^1=(-2)=-2$

b) $(-3{)}^2=(-3)\times (-3)$ $=+3\times 3$ $=+9=9$

c) $(-2{)}^{10}$ $=(-2)\times (-2)\times (-2)\times (-2)\times (-2)\times (-2)$ $\times (-2)\times (-2)\times (-2)\times (-2)$ $=+1024$ $=1024$

d) $(-1{)}^8$ $=\underset{+}{\underbrace{(-1)\times (-1)}}\times \underset{+}{\underbrace{(-1)\times (-1)}}\times \underset{+}{\underbrace{(-1)\times (-1)}}\times \underset{+}{\underbrace{(-1)\times (-1)}}$ $=(+1)\times (+1)\times (+1)\times (+1)$ $=+1$ $=1$

e) $(-1{)}^9$ $=\underset{+}{\underbrace{(-1)\times (-1)}}\times \underset{+}{\underbrace{(-1)\times (-1)}}\times \underset{+}{\underbrace{(-1)\times (-1)}}\times \underset{+}{\underbrace{(-1)\times (-1)}}$ $\times (-1)=(+1)\times (+1)\times (+1)\times (+1)\times (-1)$ $=-1$

Així podem dir que:

$(-a{)}^n=\underset{nvegades}{\underbrace{(-a)\times \dots \times (-a)}}=a^n=+b=b$ quan n és parell $(-a{)}^n=\underset{nvegades}{\underbrace{(-a)\times \dots \times (-a)}}=-(a^n)=-b$ quan n és imparell o senar

Clarament el signe menys sobreviu només si l'exponent és imparell i per tant és en el que ens hem de fixar.

Exercicis de simplificació i càlcul

1) $(-2{)}^5=$ 2) $(-3{)}^3=$ 3) $(-5{)}^2=$ 4) $(-1{)}^{888}=$ 5) $(-1{)}^{999}=$

6) $+(+1{)}^{10}=$ 7) $+(-1{)}^8=$ 8) $-(1{)}^6=$ 9) $-(-1{)}^{22}=$ 10) $-(-2{)}^7=$

Prioritats

Com que ens agrada escriure pocs parèntesis, estem obligats a fer cas dels càlculs segons aquest ordre de prioritat:

1a) Els parèntesis.

2a) potencies.

3a) Productes i divisions.

4a) Sumes i restes.

Per tant hem de fer amb prioritat unes operacions i després les de prioritat més baixa.

Exemples de productes i divisions amb sumes i restes:

Recordeu que primer es fan les multiplicacions o divisions i finalment quedarà una simple sèrie de sumes o restes.

Les multiplicacions i divisions successives es fan d'esquerra a dreta com es veu al apartat e:

a) $5+3\times 2-11\times 3-4\times 5+5$ $=5+\overbrace{3\times 2}-\overbrace{11\times 3}-\overbrace{4\times 5}+5$ $=5+6-33-20+5$ $=69$

b) $1-3+1\times (-2)\times (+3)-4+5$ $=1-3+\overbrace{1\times (-2)\times (+3)}-4+5$ $=1-3+(-6)-4+5$ $=-7$

c) $2+9÷3-3÷3+4÷2-8$ $=2+\overbrace{9÷3}-\overbrace{3÷3}+\overbrace{4÷2}-8$ $=2+3-1+2$ $=6$

d) $9-6+1\times 18÷3÷2-3+6+1$ $=9-6+\overbrace{1\times 18÷3÷2}-3+6+1$ $=9-6+3-3+6+1$ $=10$

e) $-4+24\cdot 2÷4÷3\cdot 2-1$ $=-4+\overbrace{\underbrace{24\cdot 2}÷4÷3\cdot 2}-1$ $=-4+\overbrace{\underbrace{48÷4}÷3\cdot 2}-1$ $=-4+\overbrace{\underbrace{12÷3}\cdot 2}-1$ $=-4+\overbrace{4\cdot 2}-1$ $=-4+2-1$

Exemples de potències amb productes i divisions amb sumes i restes:

Sempre té prioritat l'exponent sobre la resta d'operacions o signes:

a) $9+3^2=9+\overbrace{3^2}=9+9=18$

b) $2\cdot 3^3=2\cdot \overbrace{3^3}=2\cdot 27=54$

c) $-3^4-2=-\overbrace{3^4}-2=-(81)-2=-81-2=-83$

Exemples d'operacions amb parèntesis:

Els parèntesis són els constructors del nostre llenguatge matemàtic sense ells no podríem escriure $(-1-2)\cdot 3=-3\cdot 3=-9$ que no es el mateix que $-1-2\cdot 3=-1-6=-7,$ tampoc podríem escriure $(-2{)}^4=+16=16$ ja que no dona el mateix que $-2^4=-16$ entre d'altres expressions. Per tant les seves operacions internes van primer que la resta d'operacions del voltant. Es tracta de anar calculant de dins cap a fora.

a) $(-1-(2-5)\cdot 2)\cdot 3$ $=(-1-\overbrace{(2-5)}\cdot 2)\cdot 3$ $=(-1\overbrace{-(-3)\cdot 2})\cdot 3$ $=(\overbrace{-1+6})\cdot 3$ $=5\cdot 3$ $=15$

b) $(-1-(2-(-(3-2)+3))+2)\cdot (-(3-(4-3)+4)$ $=(-1-(2-(-(1)+3))+2)\cdot (-(3-(1)+4)$ $=(-1-(2-(-1+3))+2)\cdot (-(3-1+4))$ $=(-1-(2-(2))+2)\cdot (-(6))$ $=(-1-(2-2)+2)\cdot (-6)$ $=(-1-(0)+2)\cdot (-6)$ $=(-1-0+2)\cdot (-6)$ $=(-1+2)\cdot (-6)$ $=(1)\cdot (-6)$ $=-6$

Plànol

Resta de seccions de primer d'ESO.