Obyčajné differenciálne rovnice/Úvod do jednokrokových metód

Teraz prejdeme k numerickým metódam skn pre systémy Uvod2 skr Uvod4n (1.6) oskr skr (1.7). Vo všeobecnosti sú numerické Uvod2smetoskn založené na skr diskretizácii (rozklade) skr oblasti definície skr hľadanej funkcie na disjunktné podmnožiny. Hľadáme diskrétnych hodnôt funkcie skr hľadanej funkcie, napríklad v skn uzloch tejto dekompozície, t. j. v diskrétnych bodoch siete.

V prípade obyčajnej diferenciálnej rovnice je časový interval $(t_0,T)$ rozdelený bodmi mriežky $t_i,i=1,\dots N_h,N_h\in \mathbb{N}$ na $N_h$ podintervaly dĺžky $h_i:=t_{i+1}-t_i$, $0<h_i<T-t_0$ delené. Analýza skr numerických metód je skpravdepodobne zjednodušená, ak sa dĺžka subintervalov skr považuje za konštantnú, $h:=t_{i+1}-t_i$ potom označuje dĺžku ekvidištantného kroku. Množina všetkých uzlov tvorí numerickú sieť ${\mathrm{G}}_{\mathrm{h}}$, pričom $$G_h:=\{t_i=t_0+ih,i=1,\dots N_h\}.(3.1)$$

Ak $y(t)$ je funkcia skr presná Uvod2, potom Uvod2 získaná numerickou metosk v skn bodoch siete $t_i,i=1,\dots N_h-1$ byť určitou aproximáciou skr presnej funkcie v týchto bodoch. V postupnostiachskn sa číselná Uvod2 v bode mriežky $t_i$ označuje ako ${\eta }_i$, $${\eta }_i\approx y(t_i).$$

V kapitole 1 sme vysvetlili skn explicitnú, pozri (1.2), a skn implicitnú (1.4) Uvod2aproximáciu pomocou sks príkladom skr hodinového reťazca (tractrix). Pozícia hodín expliziten v novom časovom kroku Lösungszugang $t_{i+1}$ bola projeziert premietnutím do aktuálneho časového kroku, trojuholník vytvorený reťazcom hodín s použitím súčasných hodnôt ${\eta }_i\approx y(t_i)$ (explicitne), oskr pozícia hodín skr bolaskr premietnutá do budúcnosti, čo viedlo k implicitnému procedurálnemu pravidlu (1. 4) führte. Tieto dva nasledujúceskn Uvod2postupy zodpovedajú skn najjednoduchšiemu numerickému postupu pre diferenciálnu rovnicu (1.3) pre reťazec hodín:

Explicitná Eulerova metóda

Pre $t=t_{i+1}$ nahraďte dericia na ľavej strane skr spätným diferenciálnym kvocientom skm, $y^{\prime }(t_{i+1})\approx \frac{y(t_{i+1})-y(t_i)}{h}$, a pravú stranu vyhodnotíme v starom čase $t_i$. Pôvodná rovnica $y^{\prime }(t)=f(t,y(t))$ sa potom pre $t=t_{i+1}$ nahradí $$\frac{y(t_{i+1})-y(t_i)}{h}=f(t_i,y(t_i))$$. Túto rovnicu však vo všeobecnosti nespĺňa presne skr presne Uvod2. Teraz hľadáte skr číselný Uvod2 ${\eta }_i$, ktorý spĺňa uvedenú približnú rovnicu presne: $$\frac{{\eta }_{i+1}-{\eta }_i}{h}=f(t_i,{\eta }_i)\iff {\eta }_{i+1}={\eta }_i+hf(t_i,{\eta }_i),i=0,\dots N_h-1.(3.2)$$

Implicitná Eulerova metóda

Pre $t=t_{i+1}$ nahraďte dericia na ľavej strane skr kvocientom spätnej diferencie skm, $y^{\prime }(t_{i+1})\approx \frac{y(t_{i+1})-y(t_i)}{h}$, a pravú stranu vyhodnotíme v skm novom čase $t_{i+1}$. Výsledok je $$\frac{y(t_{i+1})-y(t_i)}{h}=f(t_{i+1},y(t_{i+1})).$$ Rovnako ako vyššie sa hľadá číselná Uvod2 ${\eta }_i$, ktorá presne spĺňa uvedenú približnú rovnicu: $$\frac{{\eta }_{i+1}-{\eta }_i}{h}=f(t_{i+1},{\eta }_{i+1})\iff {\eta }_{i+1}={\eta }_i+hf(t_{i+1},{\eta }_{i+1}),i=1,\dots N_h-1(3.3)$$

Rovnice opísané pre (explixitnú/implicitnú) Eulerovu metódu (3.2), (3. 3) nie sú presne splnené funkciou skr presnou Uvod2 $y(t)$, pretože dochádza k diskretizácii chyby v dôsledku skrátenia skn skr Taylorovým rozšírením skr dericia $y^{\prime }$. Postupným riešením týchto rovníc podľa ${\eta }_{i+1}$ sa získa iba číselný Uvod2 v skn bodoch mriežky, ${\eta }_i,i=1,\dots N_h$.

Dašie metódy

Eulerovu metódu, ako aj iné numerické metódy možno získať pomocou skr Volterrovej integrálnej rovnice (2.1) a skr numerickej kvadratúry. Ak nahradíte integrál ${\int }_{t_i}^{t_{i+1}}f(s,y(s))ds$ s skr obdĺžnikovým pravidlom, pozri obrázky 3.1, 3.2, dostanete buďskr explicitnú, aleboskr implicitnú Eulerovu metódu. Použitímskr pravidla stredového bodu pre integrál, pozri obrázok 3.3, sa získa takzvaná vylepšená Eulerova metóda (nazývaná aj explicitné pravidlo stredového bodu), $${\eta }_{i+1}={\eta }_i+hf(t_{i+\frac{1}{2}},{\eta }_{i+\frac{1}{2}}),\text{wobei}{\eta }_{i+\frac{1}{2}}:={\eta }_i+\frac{h}{2}f(t_i,{\eta }_i).(3.4)$$

Iný spôsob je skr hodnota skr funkcie $f$ v strede skr medzi $t_i,t_{i+1}$ (t. j. v $t_{i+\frac{1}{2}}:=\frac{t_i+t_{i+1}}{2}$ a v ${\eta }_{i+\frac{1}{2}}\approx y(t_{i+\frac{1}{2}})$). V tomto prípade sa na aproximáciu hodnoty sks v strede, $y(t_{i+\frac{1}{2}})$, používa krok sks explicitnej Eulerovej metódy s polovičnou dĺžkou kroku skr $\frac{h}{2}$.

Použitím lichobežníkového pravidla pre numerickú integráciu, pozri obrázok 3.4, dostaneme nasledujúcu metódusk, ktorá sa nazýva aj implicitné lichobežníkové pravidlo: $${\eta }_{i+1}={\eta }_i+\frac{h}{2}(f(t_i,{\eta }_i)+f(t_{i+1},{\eta }_{i+1})).(3.5)$$

V explicitnej variante tejto metódy, $f(t_{i+1},{\eta }_{i+1})$ je nahradené s $f(t_{i+1},{\eta }_i+hf(t_i,{\eta }_i))$ použijúc jeden krok explicitnej eulerovej metódy.
Použitím pravidla stredového bodu sa získa nasledujúcask metóda, ktorá je tiež
implicitné pravidlo stredového bodu sa nazýva: $${\eta }_{i+1}={\eta }_i+hf(t_{i+1/2},\frac{{\eta }_i+{\eta }_{i+1}}{2}).(3.6)$$

Iný explicitný variant skr, $\frac{{\eta }_i+{\eta }_{i+1}}{2}$ by sa vypočítal polovičným krokom explicitnej Eulerovej metódy sks s ${\eta }_i+\frac{h}{2}f(t_i,{\eta }_i)$ ersetzen, siehe (3. 6).

Ilustrácia 3.1: Explicitné obdĺžnikové pravidlo pre aproximáciu integrálu sks $I[f(x)]={\int }_a^{b}f(x)dx$ s kvadratúrnym uzlom $x_0=a$.

Ilustrácia 3.2: Implicitné pravidlo obdĺžnika na aproximáciu sks Integrals $I[f(x)]=\underset{a}{\overset{b}{\int }}f(x)dx$ mit einem Quadraturknoten $x_0=b$.

Jednokrokové a viackrokové metódy

Práve opísané numerické prístupy Uvod2s vyžadujú na výpočet hodnoty funkcie sks v novom bode mriežky nasledovn $t_{i+1}$ len skn predchádzajúcu hodnotu z $t_i$. Takéto postupy nazývame sk0 (ESV). Na druhej strane sk1 (MSV) využíva aj informácie z niekoľkých predchádzajúcich krokov $t_i,t_{i-1},\dots ,t_{i-k+1}$, kde $k$ je tu pevne stanovené (k-kroková metóda).

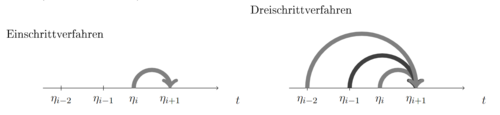Obrázok schémy pre jednokrokovú a trojkrokovú metódu.

In diesem Kapitel werskn wir numerische Uvod2sformeln für die sk0 und skren Diskretisierungsfehler untersuchen. Budeme sa zaoberať len tými numerickými metódami, ktoré dostatočne dobre aproximujú presný Uvod2.

Obr. 3.3: Pravidlo stredového bodu pre aproximáciu integrálu $I[f(x)]=\underset{a}{\overset{b}{\int }}f(x)dx$ s uzlom $x_0=\frac{a+b}{2}$.

---

Definícia 3.1 (Explicitná jednokroková metóda)

Daná je na dĺžka ekvidistantného kroku $0<h\le T-t_0$, a numerická sieť $G_h$, pozri (3.1). Explicitná jednmoktoková metóda je daná nasledujúcim iteračným predpisom,
${\eta }_{i+1}={\eta }_i+h\mathrm{\Phi }(t_i,{\eta }_i;h;f),i=0,\dots ,N_h-1,(3.7)$

kde $\mathrm{\Phi }(\cdot ,\cdot ;h;f):\{G_h-t_{N_h}\}\times {ℝ}^m\to {ℝ}^m$ je funkcia metódy (predpisu).

---

Príklad 3.1

Funkcia metódy pre explicitnú Eulerovu metódu je $\mathrm{\Phi }(t,y;h;f)=f(t,y),$ a pre vylepšenú (modifikovanú) Eulerovu metódu (3. 4) $\mathrm{\Phi }(t,y;h;f)=f(t+\frac{h}{2},y+\frac{h}{2}f(t,y)).$ $\diamond$

Obr. 3.4: Trapézové pravidlo pre aproximáciu integrálu sks $I[f(x)]=\underset{a}{\overset{b}{\int }}f(x)dx$ s dvoma uzlami $x_0=a,x_1=b.$

Príklad 3.2

Riešime jednoduchú úlohu Uvod4 $y^{\prime }=y,y(0)=1$ pomocou explicitnej Eulerovej metódy s konštantným krokom $h=\frac{T}{N_h}$.
Numerické riešenie je: $\begin{array}{ccc}{\eta }_0& =& 1,\\ {\eta }_1& =& 1+hf(t_0,{\eta }_0)=1+h{\eta }_0=1+h,\\ {\eta }_2& =& {\eta }_1+hf(t_1,{\eta }_1)=1+h+h{\eta }_1\\ & =& 1+h+h(1+h)=(1+h{)}^2,\\ {\eta }_3& =& {\eta }_2+hf(t_2,{\eta }_2)\\ & =& (1+h{)}^2+h{\eta }_2=(1+h{)}^3,\\ & \dots & \end{array}$

Matematickou indukciou možno ukázať, že ${\eta }_i=(1+h{)}^i,i=1,\dots N_h$. Z toho vyplýva, že ${\eta }_{N_h}=(1+\frac{T}{N_h}{)}^{N_h}$ konverguje k $e^T$ pre $N_h\to \mathrm{\infty }$. To zodpovedá presnému riešeniu $y(T)$. To znamená, že numerické riešenie v určitom časovom bode $t=T$ konverguje k presnej hodnote tomto časovom bode pre veľkosť kroku $h$ idúcu k nule. $\diamond$.