Obyčajné differenciálne rovnice/Implicitné Runge-Kutta metódy

4.3 Implicitné Runge-Kutta metódy

Ak je matica koeficientov $A$ v Butcherovej tabuľke Rungeho-Kuttovej metódy plne vyplnenou maticou, výpočet ohodnotení funkcie $k_j$ pre každé $j=1,\dots ,s$ závisí od ostatných $k_1,\dots k_s$, najmä tiež od $k_j,k_{j+1},\dots k_s$ , pozri (4. 1). Najjednoduchšou iRKV je už známa implicitná Eulerova metóda, ďalšími príkladmi sú implicitný stredový bod a lichobežníkové pravidlo:

Implicitné pravidlo stredového bodu, $s=1$:

$\begin{array}{ccc}{k}_1& =& f(t_i+\frac{h}{2},{\eta }_i+\frac{h}{2}{k}_1)\\ {\eta }_{i+1}& =& {\eta }_i+h{k}_1\end{array}$

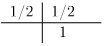
Implicitné lichobežníkové pravidlo, $s=2$:

$\begin{array}{ccc}{k}_1& =& f(t_i,{\eta }_i)\\ k_2& =& f(t_i+h,\underset{{\eta }_{i+1}}{\underbrace{{\eta }_i+\frac{h}{2}(k_1+k_2)}})\\ {\eta }_{i+1}& =& {\eta }_i+\frac{h}{2}(k_1+k_2)\\ & \equiv & {\eta }_i+\frac{h}{2}(f(t_i,{\eta }_i)+f(t_{i+1},{\eta }_{i+1})).\end{array}$

Dôležitou podmnožinou iRKV sú tzv. gaussovské metódy, ktoré umožňujú čo najväčší poriadok vzhľadom na počet krokov. Tieto metódy patria medzi takzvané kolokačné metódy a sú odvodené od Gaussovej kvadratúry, ktorej vďačia za svoj názov. Gaussove metódy, ako aj iné (ale nie všetky) iRKV, majú dobré stabilizačné vlastnosti, ktoré sú dôležité najmä pri „tuhých“ problémoch.

Stiff problémy

Pojem tuhý problém vznikol pri použití numerických metód na riešenie diferenciálnej rovnice, keď sa na získanie použiteľného konvergentného riešenia vyžadujú veľmi malé veľkosti krokov alebo menšie a menšie veľkosti krokov s postupom metódy. V takýchto prípadoch explicitné metódy, ako napríklad Eulerova metóda alebo eRKV vyššieho rádu s pevnou veľkosťou kroku, zlyhávajú; metódy s riadením veľkosti kroku vytvárajú stále menšie veľkosti kroku až po nulu (v rámci presnosti počítača), čo znamená, že v určitom bode sa už nepohybujú, zastavia sa - odtiaľ pochádza termín „tuhý“.

Medzi tuhé problémy patria diferenciálne rovnice s riešeniami s vysokou rýchlosťou zmien alebo systémy so zložkami riešenia, ktoré rastú veľmi rozdielnou rýchlosťou. Tu explicitná metóda generuje aproximáciu riešenia v ďalšom časovom kroku na základe predchádzajúcich, vo vysoko dynamických systémoch už nie aktuálnych, sklonov/informácií náchylných na chyby, a tak explicitná metóda rýchlo prekročí cieľ.

Príkladom tuhých problémov sú systémy lineárnych diferenciálnych rovníc, ktorých matica má veľmi rozdielne vlastné hodnoty, alebo diferenciálne rovnice opisujúce chemické reakcie s látkami, ktoré reagujú rôznymi rýchlosťami. Vďaka dobrým stabilizačným vlastnostiam implicitných jednokrokových metód, ktoré svoj priebeh v aktuálnom kroku prispôsobujú budúcemu (ešte silnejšiemu) gradientu, a tak poskytujú dobré výsledky aj pre väčšie veľkosti krokov $h$, sú iRKV vhodné najmä pre tuhé problémy.

Obrázok 4.1: Komponenty riešenia systému tuhej diferenciálnej rovnice, presné riešenie $y_1(t)=e^{10t},y_2=1000e^{-10t}$ a aproximácia explicitnou Eulerovou metódou, $h=0.125$.

Pri implicitných Runge-Kutta metódach sa kroky $k_j$ počítajú riešením sústavy rovníc (4.1). Existencia riešenia tejto prípadne nelineárnej sústavy rovníc nie je vždy zaručená alebo dosiahnuteľná pomocou iteračných metód. Postačujúcou podmienkou existencie takéhoto riešenia a konvergencie iteračnej metódy pevného bodu je dostatočne malá veľkosť kroku $h$:

---

Nastavenie 4.2 (Butcher 1964)

Nech $f$ je spojitý na $ℝ\times {ℝ}^m$ a Lipschitzovo spojitý vzhľadom na $y$ s Lipschitzovou konštantou $L$. Pre prírastok $h$ platí $h<\frac{1}{L\Vert |A\Vert {|}_{\mathrm{\infty }}}=\frac{1}{L{\mathrm{m}\mathrm{a}\mathrm{x}}_i\sum _{j=1,\dots s}|a_{ij}|}.(4.12)$

Potom sústava rovníc (4.1), $k_j=f(t_i+h{c}_j,{\eta }_i+h\sum _{\nu =1}^s{a}_{jm}{k}_{\nu })j=1,\dots ,s$

je jedinečné riešenie, ktoré sa dá vypočítať postupnou substitúciou (iteráciou pevného bodu). Ak $f\in C^p(ℝ\times {ℝ}^m)$, potom $k_j$ ako funkcie $h$ sú tiež $p$-krát spojito diferencovateľné.

Dôkaz. Pre jednoduchosť nech $m=1$. Riešenie (nelineárnej) sústavy rovníc (4.1) pre $k_1,\dots k_s$ možno určiť iteračne: $k_j^{(m+1)}=f(t_i+h{c}_j,{\eta }_i+h\sum _{\nu =1}^s{a}_{j\nu }{k}_{\nu }^{(m)})j=1,\dots ,s.(4.13)$

Ak sústavu rovníc (4.1) prevedieme do vektorového tvaru, $\overrightarrow{K}=F(\overrightarrow{K}),$

pričom $\overrightarrow{K}=(k_1,\dots k_s{)}^T\in {ℝ}^s,F:{ℝ}^s\to {ℝ}^s,$ $\begin{array}{c}{F}_j(\overrightarrow{K}):=f(t_i+h{c}_j,{\eta }_i+h\sum _{\nu =1}^s{a}_{j\nu }{k}_{\nu })=f(t_i+h{c}_j,{\eta }_i+h{A}_j\cdot \overrightarrow{K})j=1,\dots ,s\end{array}$

namiesto (4.13) dostaneme iteračné pravidlo ${\overrightarrow{K}}^{(m+1)}=F\left({\overrightarrow{K}}^{(m)}\right)(4.14)$

s počiatočným vektorom $K^{(0)}.$

Podľa Banachovej vety o pevnom bode, pozri vetu 2.1, kapitola 2, existuje jedinečné riešenie, pevný bod $\overrightarrow{K}=F(\overrightarrow{K})$, ak $F$ je samomapovanie a kontrahovanie. Pre funkciu $F:{ℝ}^s\to {ℝ}^s$ platí, že $F({ℝ}^s)\subseteq {ℝ}^s$, t. j. vždy je samomapovanie.
Teraz skúmame, či $F$ je kontrakcia. Odhadneme Lipschitzovu spojitosť funkcie $f$ a trojuholníkovú nerovnosť pre absolútnu hodnotu v maximálnej norme: $\begin{array}{c}\Vert F(\overrightarrow{K}{)}^1-F({\overrightarrow{K}}^2){\Vert }_{\mathrm{\infty }}=\underset{j=1,...,s}{\max }|f(t_i+h{c}_j,{\eta }_i+h\sum _{\nu =1}^s{a}_{j\nu }{k}_{\nu }^1)-f(t_i+h{c}_j,{\eta }_i+h\sum _{\nu =1}^s{a}_{j\nu }{k}_{\nu }^2)|\\ \stackrel{L-stetig}{\le }\underset{j}{\max }hL|\sum _{\nu =1}^s{a}_{j\nu }(k_{\nu }^1-k_{\nu }^2)|\le hL\underset{j}{\max }\sum _{\nu =1}^s|a_{j\nu }|\underset{\nu }{\max }|k_{\nu }^1-k_{\nu }^2|\\ =hL\Vert |A\Vert {|}_{\mathrm{\infty }}\Vert K^1-K^2{\Vert }_{\mathrm{\infty }}.\end{array}$

Z tohto odhadu vyplýva, že $F$ je kontrakcia v Banachovom priestore ${ℝ}^s,\Vert \cdot {\Vert }_{\mathrm{\infty }}$, ak $hL\Vert A\Vert {|}_{\mathrm{\infty }}\Vert <1$. Z toho vyplýva, že mapovanie $F$ pre $h<1/(L\Vert |A\Vert {|}_{\mathrm{\infty }})$ v ${ℝ}^s$ má jedinečný pevný bod, ${\overrightarrow{K}}^{\star }=F({\overrightarrow{K}}^{\star }),$

Tvrdenie (4.13), (4.14) konverguje k tomuto pevnému bodu. Tvrdenie o p-násobnej spojitej diferencovateľnosti $k_j$ ponecháme bez dôkazu. ◻

---

'Poznámka o riešiteľnosti iRKV Remark on the solvability of the iRKV

1. Obmedzenie veľkosti kroku $h$ môže byť veľmi obmedzujúce pre veľké $L$ konštanty (t. j. pre $f$ s vysokými hodnotami derivácie $\frac{\partial f}{\partial y}\approx L$) môžu byť veľmi obmedzujúce a viesť k pomalej konvergencii metódy pevného bodu. Východiskom v týchto prípadoch je použitie inej iteračnej metódy s vyššou rýchlosťou konvergencie na výpočet $k_j$, napríklad Newtonovej, sekantovej alebo kvázi-Newtonovej metódy. Tieto metódy konvergujú aj pre väčšie $h$, pretože majú superlineárnu rýchlosť konvergencie, ak je počiatočná hodnota zvolená priaznivo, v rámci tzv. konvergenčného intervalu.
2. Ak je funkcia $f$ len lokálne Lipschitzovo spojitá v $y$, t. j. len v okolí $K^{(0)}$, potom vyplývajú ďalšie obmedzenia na veľkosť kroku $h$, aby sa zaručila vlastnosť samomapovania.
3. Lipschitzova spojitosť procesnej funkcie $\mathrm{\Phi }$ eRKV, ako aj iRKV vzhľadom na $y$ vyplýva z Lipschitzovej spojitosti $f$. To znamená, že iRKV s rádom konzistencie p sú tiež konvergentné s rádom konvergencie p. (pozri vetu 3.1)