Obyčajné differenciálne rovnice/Úvod do Runge-Kutta metód

Runge-Kutta metódy

Metódy Runge-Kutta (RKV) sú špeciálne jednokrokové metódy, ktoré vďaka svojej štruktúre umožňujú vyšší stupeň konzistencie, a tým aj vyššiu presnosť numerického riešenia. Tieto metódy vyvinul nemecký matematik Wilhelm Kutta v roku 1901 na základe článku Carla Rungeho z roku 1895.

Ak sa pozrieme na rovnicu $y^{\prime }(t)=f(t,y(t))$, vyšší rád konzistencie metódy Runge-Kutta je spôsobený vyšším počtom vyhodnotení funkcie $f$ (pravá strana rovnice) v bodoch medzi $t_i$ und $t_{i+1}=t_i+h$ dosiahnuté. Medziľahlé body $t_i+ch$ voláme Kroky, oder Body podpory, pričom $c\in [0,1]$ a $h$ je prírastok.

V doteraz študovaných ESV, ako sú Eulerova metóda, lichobežníkové pravidlo, pravidlo stredového bodu (v explicitnej alebo implicitnej forme), sa v každom kroku použilo jedno alebo dve vyhodnotenia $f$ v bodoch $t_i,t_{i+1/2}$ alebo $t_{i+1}$. V RKV sa počet bodov mriežky zvyšuje a ich poloha sa určuje primerane, aby sa dosiahol čo najvyšší poriadok konzistencie. Die bisher bekannten ESV können als die einfachsten Runge-Kutta Verfahren einordnet werden.

---

'Definícia 4.1. ("Runge-Kutta metóda").

Nech $s\in \mathbb{N}$ je počet stupňov/podporných bodov, $A\in {ℝ}^{s\times s}$ je koeficientová matica so zápismi $(A{)}_{j,m}=:a_{jm}$, nech $\overrightarrow{b}\in {ℝ}^s$ vektor váh a $\overrightarrow{c}\in {ℝ}^s$ vektor výberových bodov.
Metóda s pravidlom $$\begin{array}{cc}{\eta }_0& =y_0,\\ k_j& =f(t_i+h{c}_j,{\eta }_i+h\sum _{m=1}^s{a}_{jm}{k}_m)\text{für}j=1,\dots ,s,(4.1)\\ {\eta }_{i+1}& ={\eta }_i+h\sum _{j=1}^s{k}_j{b}_j\text{für}i=0,1,\dots ,N_h-1\end{array}(4.2)$$ sa nazýva s-kroková Runge-Kutta metóda.

---

Metódy Runge-Kutta sa dajú špecifikovať aj schematicky v takzvanej Butcherovej tabuľke:

oder kurz

$\overrightarrow{c}=\left(\begin{array}{c}{c}_1\\ ⋮\\ c_s\end{array}\right),{\overrightarrow{b}}^T=(b_1,\dots b_s)$.

Príklad 4.1.

Ohodnotenie funkcie $k_j$ RKV pre $j=2$ je $k_2=f((t_i+h{c}_2,{\eta }_i+h\sum _{m=1}^s{a}_{2m}{k}_m)=f((t_i+h{c}_2,{\eta }_i+h{\overrightarrow{a}}_2\cdot \overrightarrow{k}),$ kde ${\overrightarrow{a}}_2=(a_{21},\dots ,a_{2s})$ je druhý riadok matice $A$ a ${\overrightarrow{k}}_2=(k_1,\dots ,k_s)$ $\diamond .$

Nová hodnota numerického riešenia po jednom kroku RKV (nazývanom aj Runge-Kutta aktualizácia) sa vypočíta podľa (4.2) ako ${\eta }_{i+1}={\eta }_i+h\sum _{j=1}^s{k}_j{b}_j.$ Porovnanie tejto rovnice s Volterrovou integrálnou rovnicou (2.1) na intervale $(t_i,t_{i+1})$, $y(t_i+h)=y(t_i)+\underset{t_i}{\overset{t_{i+1}}{\int }}f(s,y(s))ds$ vedie k nasledujúcim úvahám: Ak integrál ${\int }_{t_i}^{t_{i+1}}f(s,y(s))ds$ zmysluplne nahradíme súčtom takým, že $h\sum _{j=1}^s{k}_j{b}_j\approx \underset{t_i}{\overset{t_{i+1}}{\int }}f(s,y(s))ds,$ na výpočet novej hodnoty $f$ sa použije kvadratúra ${\eta }_{i+1}$. Tu $k_j$ sú $s$ uzly tejto kvadratúry v bodoch mriežky $t_i+h{c}_j$ (pozri (4.1)) a $b_j$ sú váhy kvadratúry. Skonštruovať RKV teda znamená nájsť vhodnú kvadratúru integrálu ${\int }_{t_i}^{t_{i+1}}f$. Najjednoduchšie RKV (ide o jednokrokové metódy uvedené v kapitole 3) zahŕňajú aplikáciu kvadratúr, ako je pravidlo obdĺžnika, stredového bodu a lichobežníka pre integrál ${\int }_{t_i}^{t_{i+1}}f(s,y(s))ds$ (pozri poznámku 3.1 bod iii) a obrázky 3.1, 3.2, 3.3, 3.4). Butcherovu tabuľku možno interpretovať takto: Vektor $\overrightarrow{c}$ opisuje body mriežky a vektor $\overrightarrow{b}$ opisuje váhy príslušnej kvadratúry $f$ na intervale $(t_i,t_{i+1})$. Die Matrix $A$ spiegelt in gewissem Sinne die Differentialgleichung zurück. Dies kann wie folgt begründet werden:
Nach der Definition der Runge-Kutta Verfahren, siehe (4. 1), und mithilfe der Differentiagleichung $y^{\prime }=f(t,y)$ kann darauf geschlossen werden, dass die $k_j$ die Ableitungen der gesuchten Funktion an den Stützstellen $t_i+h{c}_j$ approximieren, sodass mit $j=1,\dots s$ und $i$ - fest, $$k_j\approx y^{\prime }(t_i+h{c}_j)$$

platí. Keďže na výpočet $A$ sa používa matica $k_j$, automaticky sa tým vyjadruje diferenciálna rovnica vo vyššie opísanom zmysle.

Na rozlíšenie explicitných a implicitných metód RK možno použiť maticu $A$:

• Explicitná Runge-Kutta metóda (eRKV):
  

Ak je matica $A$ dolná trojuholníková matica, ide o explicitnú RKV. V tomto prípade sa v každom $k_1,\dots ,k_{j-1}$ kroku na výpočet $t_i$ použije iba predtým vypočítaná $k_j,j=1,\dots s$. V tomto prípade môžete explicitne vypočítať $k_j$ vložením ako $$k_j=f(t_i+h{c}_j,{\eta }_i+h\sum _{m=1}^{j-1}{a}_{jm}{k}_m).$$

• 'Implicitná Runge-Kutta metóda (iRKV):
  Implicitná Runge-Kutta metóda (iRKV):
  

Ak je matica $A$ plne vyplnená matica, potom $k_j$ všeobecne závisí od všetkých $k_1,\dots ,k_s$ pre každé $j=1,\dots s$. Výpočet $k_j$ sa potom vykoná riešením (lineárnej alebo prípadne nelineárnej) sústavy rovníc. V tomto prípade je výpočet $k_j$ jednoduchší alebo lacnejší, ak $A$ je trojuholníková matica. V tomto prípade sa rozlišuje medzi

• • DIRK-metóda: ’diagonálna implicitná metóda RK’:
    

Matrix $A$ je trojuholníková matica s $diag(A)\ne \mathrm{𝟎}$,

• • SDIRK-metóda: ’jednoducho diagonálna implicitná metóda RK’:
    

matica $A$ je trojuholníková matica s $diag(A)=\lambda diag(I)\ne \mathrm{𝟎},\lambda \in ℝ,I$ ist eine Einheitsmatrix,

• • SIRK-metóda ’jednoducho implicitný postup RK’:
    

matica $A$ je plne vyplnená matica, pričom $diag(A)=\lambda diag(I)$ a horná trojuholníková matica tiež pozostáva z $\lambda$'s.

Teraz uvedieme niekoľko konkrétnych príkladov Runge-Kutta metód:
Explicitná Eulerova metóda, $s=1$:

$$\begin{array}{c}\\ k_1& =f(t_i+0.h,{\eta }_i+0.h{k}_1)=f(t_i,{\eta }_i)\\ {\eta }_{i+1}& ={\eta }_i+h{k}_1\equiv {\eta }_i+hf\underset{=k_1}{\underbrace{(t_i,{\eta }_i)}}\end{array}$$
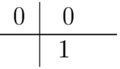
Implicitná Eulerova metóda, $s=1$:

$$\begin{array}{c}\\ k_1& =f(t_i+1.h,{\eta }_i+1.h{k}_1)\\ {\eta }_{i+1}& ={\eta }_i+h{k}_1\equiv \mathrm{\%}{\eta }_i+hf\underset{=k_1}{\underbrace{(t_i+h,{\eta }_i+h{k}_1)}}={\eta }_i+hf(t_i+h,\underset{={\eta }_{i+1}}{\underbrace{{\eta }_i+h{k}_1}})\end{array}$$
Vylepšená Eulerova metóda (explicitné pravidlo stredového bodu), $s=2$:

$$\begin{array}{cc}{k}_1& =f(t_i,{\eta }_i)\\ k_2& =f(t_i+\frac{h}{2},{\eta }_i+\frac{h}{2}{k}_1)\\ {\eta }_{i+1}& ={\eta }_i+h(0.k_1+1.k_2)\\ & \equiv {\eta }_i+hf\underset{=k_2}{\underbrace{(t_i+\frac{h}{2},{\eta }_i+\frac{h}{2}\underset{=k_1}{\underbrace{f(t_i,{\eta }_i)}})}}\end{array}$$

Klasický Runge-Kutta postup, $s=4$:

$$\begin{array}{cc}{k}_1& =f(t_i,{\eta }_i)\\ k_2& =f(t_i+\frac{h}{2},{\eta }_i+\frac{h}{2}{k}_1)\\ k_3& =f(t_i+\frac{1}{2}h,{\eta }_i+\frac{h}{2}{k}_2)\\ k_4& =f(t_i+h,{\eta }_i+h{k}_3)\\ {\eta }_{i+1}& ={\eta }_i+h(\frac{k_1}{6}+\frac{k_2}{3}+\frac{k_3}{3}+\frac{k_4}{6})\end{array}$$

$3/8$- Pravidlo, $s=4$:

$$\begin{array}{cc}{k}_1& =f(t_i,{\eta }_i)\\ k_2& =f(t_i+\frac{h}{3},{\eta }_i+\frac{h}{3}{k}_1)\\ k_3& =f(t_i+\frac{2}{3}h,{\eta }_i-\frac{h}{3}{k}_1+h{k}_2)\\ k_4& =f(t_i+h,{\eta }_i+h{k}_1-h{k}_2+h{k}_3)\\ {\eta }_{i+1}& ={\eta }_i+h(\frac{k_1}{8}+\frac{3}{8}{k}_2+\frac{3}{8}{k}_3+\frac{k_4}{8})\end{array}$$

Ďalšie dve explicitné 3-stupňové RKV sú dané nasledujúcimi Butcherovými tabuľkami:

Heunova metóda, $s=3$ (1900): $$3-stupňová eRKV